Input File Configuration

Integrator

The HiRep code uses a multilevel integrator and each integrator level has to be specified in the input file.

    integrator {
        level = 0
        type = o2mn
        steps = 10
    }

Variable	Description
`level`	unique integrator level (level 0 is the outermost level)
`type`	integrator type (see below)
`steps`	number of integration steps

The table below show the different integrators implemented in the HiRep code. The last column in the table show how many times the next integrator level will be called in each iteration of the given integrator.

Type	Description	Next level calls
`lf`	leap-frog integrator	1
`o2mn`	2nd order minimal norm (omelyan) integrator	2
`o4mn`	4th order minimal norm (omelyan) integrator	5

Plaquette gauge

This gauge monomial is the standard Wilson plaquette action.

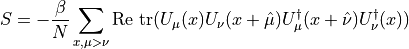
$S = -\frac{\beta}{N}\sum_{x,\mu>\nu} \textrm{Re}~\textrm{tr}(U_\mu(x)U_\nu(x+\hat{\mu})U_\mu^\dagger(x+\hat{\nu})U_\nu^\dagger(x))$

The following example shows how to specify a gauge monomial in the input file.

    monomial {
        id = 0
        type = gauge
        beta = 2.0
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`beta`	bare coupling for the gauge field
`level`	integrator level where the monomial force is evaluated

Lüscher-Weisz gauge

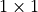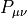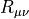This gauge monomial is the Lüscher-Weisz (tree-level Symanzik) gauge action, including the $1\times1$ plaquettes $P_{\mu\nu}$ and the $1\times2$ rectangular loops $R_{\mu\nu}$ . The two coefficients below are related through $c_0+8c_1=1$ to ensure the correct continuum limit.

$S = -\frac{\beta}{N}\sum_{x,\mu>\nu} c_0\textrm{Re}~\textrm{tr}[P_{\mu\nu}(x)] + c_1\textrm{Re}~\textrm{tr}[R_{\mu\nu}(x)+R_{\nu\mu}(x)]$

Specify a gauge monomial in the input file as in the following example:

    monomial {
        id = 0
        type = lw_gauge
        c0 = 1.666667
        beta = 2.0
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`beta`	bare coupling for the gauge field
`c0`	coefficient in front of the plaquette term
`level`	integrator level where the monomial force is evaluated

HMC Parameters

The HMC monomial is the standard term for simulating two mass degenerate fermions.

$S = \phi^\dagger(D^\dagger D)^{-1}\phi\,,$

corresponding to the following input file configurations with example parameters:

    monomial {
        id = 1
        type = hmc
        mass = -0.750
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 5
        level = 1
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

Twisted Mass

In this monomial the twisted mass is added before the Dirac operator has been even/odd preconditioned. Specify as follows:

    monomial {
        id = 1
        type = tm
        mass = -0.750
        mu = 0.1
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 5
        level = 1
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`mu`	bare twisted mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

Twisted Mass Alternative

In this monomial the twisted mass is added after the Dirac operator has been even-odd preconditioned.

    monomial {
        id = 1
        type = tm_alt
        mass = -0.750
        mu = 0.1
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 5
        level = 1
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`mu`	bare twisted mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

Hasenbusch

The Hasenbusch term is a mass preconditioned term, used in connection with an HMC monomial.

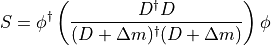
$S = \phi^\dagger\left(\frac{D^\dagger D}{(D+\Delta m)^\dagger (D+\Delta m)}\right)\phi$

    monomial {
        id = 1
        type = hasenbusch
        mass = -0.750
        dm = 0.1
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 2
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`dm`	shift in the bare mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

TM Hasenbusch

To include a Hasenbusch monomial with even-odd preconditioned twisted mass, adjust starting from the following template parameters

    monomial {
        id = 1
        type = hasenbusch_tm
        mass = -0.750
        mu = 0
        dmu = 0.1
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 2
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`mu`	twisted mass
`dmu`	shift in the twisted mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

TM Hasenbusch Alternative

For a twisted even-odd preconditioned operator use the type hasenbusch_tm_alt.

    monomial {
        id = 1
        type = hasenbusch_tm_alt
        mass = -0.750
        mu = 0
        dmu = 0.1
        mt_prec = 1e-14
        force_prec = 1e-14
        mre_past = 2
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`mu`	bare twisted mass
`dmu`	shift in the twisted mass
`mt_prec`	inverter precision used in the Metropolis test
`force_prec`	inverter precision used when calculating the force
`mre_past`	number of past solutions used in the chronological inverter
`level`	integrator level where the monomial force is evaluated

RHMC

The RHMC monomial uses a rational approximation to simulate an odd number of mass degenerate fermions.

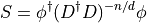
$S = \phi^\dagger(D^\dagger D)^{-n/d}\phi$

Include this in the input file using the type rhmc. One further needs to specify numerator and denominator fractions in the rational approximation.

    monomial {
        id = 1
        type = rhmc
        mass = -0.750
        n = 1
        d = 2
        mt_prec = 1e-14
        md_prec = 1e-14
        force_prec = 1e-14
        level = 0
    }

Variable	Description
`id`	unique monomial id
`type`	monomial type
`mass`	bare fermion mass
`n`	fraction numerator
`d`	fraction denominator
`mt_prec`	inverter precision used in the Metropolis test
`md_prec`	precision of the rational approximation
`force_prec`	inverter precision used when calculating the force
`level`	integrator level where the monomial force is evaluated

Chronological Inverter

When using the chronological inverter the force precision should be 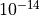$10^{-14}$ or better to ensure reversibility in the algorithm. Further, masses given in monomials should include the mass shift.